以下内容都基于学习ZK知识进行有限且抽象讲解，目的是为了让13岁以上的人轻松理解，如果需要深入学习有限域，可以查看WIKI-有限域

术语补充

• 有限域：有限域是一个包含有限个元素的集合（封闭性），这个集合上定义了加法和乘法运算，满足域的公理。
• 域：域是一个集合，上面定义了加法和乘法运算，满足以下公理：
  • 加法满足交换律、结合律、存在零元、存在加法逆元
  • 乘法满足交换律、结合律、存在单位元素、非零元素存在乘法逆元
  • 乘法对加法满足分配律
• 符号：
  • $F_q$：表示一个大小为 $q$ 的有限域，这个 $q$ 被称为有限域的阶，它是一个素数的幂次方

有限域

观察下面这个图片

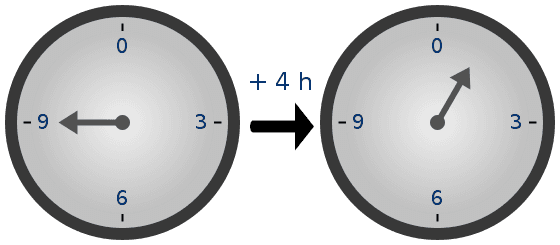
很简单的一个时钟，实际上很好地展示了有限域的加法运算工作机制，钟表上的数字就是有限域中的元素，钟表指针的移动就是有限域中的加法运算。时钟到达 12 时会转换为 0 ，然后继续循环，可以理解为有限域元素的计算会在元素集合内循环，这体现了有限域的加法封闭性。

他就像是三体中的星环城，无论你走多远，最终都会回到原点。

实际上，我们可以简单理解为，有限域元素的所有的运算对结果都进行了一个模（mod）运算。 ( 4 + 9 = 13, 13 mod 12 = 1)，无论是加减乘除，结果都需要取模。

对于乘法运算，由于有限域的阶是素数的幂，那么它的乘法群一定是循环群，这个性质对于ZK证明系统非常重要。我们在乘法循环群小节中详细介绍。